The Levitation of Magneto

Magneto first debuted in “The X-men#1” and is one of the most iconic X-men supervillains. Magneto is a mutant and goes by the nickname ‘the master of magnetism’. The powers of magneto are astounding. He can manipulate any magnetic field and therefore also every electric field. Besides throwing iron bars at his enemies, we can see that he can levitate many things, even non-magnetic things like himself. In this post I will show how Magneto can levitate himself and calculate what kind of magnetic field he needs to produce.

First we need to know how Magneto can levitate himself. As most people will know humans aren’t typically magnetic like iron bars. There are many different kinds of magnetism. The most common are diamagnetism, paramagnetism and ferromagnetism. The last one is the one that most people are familiar with. Ferromagnetic materials have their magnetic fields spontaneously aligned and then form permanent magnets. Many magnets encountered in your daily life, like your magnets on the refrigerator, are ferromagnetic. The second kind of magnetism, paramagnetism, is weaker than ferromagnetism and exists in materials with unpaired electrons. Both ferromagnetic materials and paramagnetic materials will be attracted to other magnetic fields, so Magneto will not be able to levitate with ferromagnetism and paramagnetism. Another argument is that humans (and probably mutants too) aren’t paramagnetic or ferromagnetic because of our atomic composition. So the last option is diamagnetism. Diamagnetism is very weak and only observable in absence of ferromagnetism and paramagnetism. Every material is diamagnetic and diamagnetic materials will be repelled by other magnetic fields. Researches at the university of Nijmegen have successfully levitated frogs with the help of diamagnetism. So it looks like Magneto will probably levitate himself with diamagnetism.

The Bohr-Van Leeuwen theorem states that classically magnetism can’t exist in thermal equilibrium, so magnetism is a purely quantum mechanical effect. When an external magnetic field is applied the electrons in the material will describe a currentloop which induces an opposite magnetic field. To get the correct description of diamagnetism you will need to use quantum mechanics. This can be done by using perturbation theory on the hamiltonian of an electron in a magnetic field. Diamagnetism is a pure quantum mechanical effect but there’s a classical description known as Landau magnetism that uses the idea of electrons describing current loops. Both methods will give you the same expression for the magnetic dipole moment induced by a magnetic external field due to diamagnetism. So Magneto will produce an external magnetic field to induce a magnetic moment in his body and therefore will be repelled by the magnetic field.

To deduce what kind of magnetic field Magneto needs to produce we will make the following assumptions to simplify things. First we will assume disrespectfully Magneto to be a point particle and that he can only move in one dimension, namely the z-direction. The restriction to one dimension will greatly simplify things, because the stability of the levitation point becomes very easy. Magneto will create a non-uniform magnetic field along the z-axis, due to this he will induce a magnetic moment within himself and will be repelled due to diamagnetic effects. In the next picture there is a schematic drawing of the situation. In the drawing Magneto is an ellipse, but that’s just for clarity. We will still assume he is a point particle.

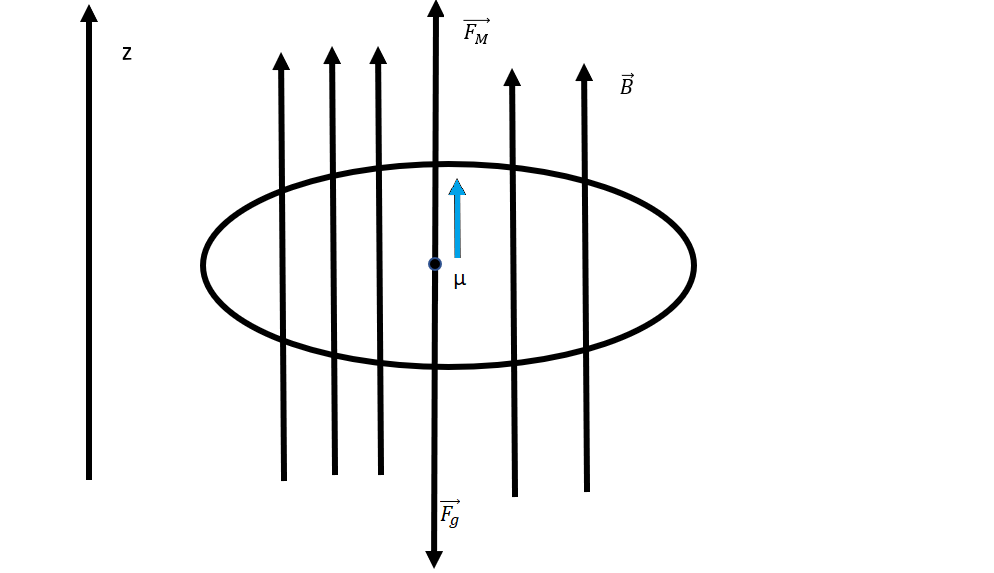
So we have a body with a magnetic moment (mu) induced by the magnetic field (B). The magnetic moment then feels an upward force due to the magnetic field. Gravity also acts as a downward force on the body. First we need to find the diamagnetic force acting on Magneto. When a magnetic moment is placed in a magnetic field it gets potential energy (U) according to:

$U = -\vec{\mu}\cdot\vec{B}$

The magnetic moment of Magneto is build up as two parts. First he has an own magnetic moment, when the magnetic field is absent, and secondly he has a magnetic moment induced by the magnetic field. The first magnetic moment is material specific and humans tend not be ferromagnetic. So we can safely assume that the own magnetic moment is zero. The magnetic moment induced due to diamagnetism can be calculated with quantum mechanics and is:

$\vec{\mu}=-\frac{Ze^2\vec{B}}{6m_e}\langle r^2\rangle$

Where Z are the number of electrons present, e is the elementary charge, m_e is the mass of the electron and <r^2> is a quantummechanical expactation value. A force can typically be characterised as the gradient of a potential field. A force will try to push an object to a lower potential energy. Think of a marble rolling of a hill in a gravitational field. On top of the hill it has a high potential energy and due to gravity it will be pushed downward, where the potential energy is lower. So our diamagnetic force is the gradient of our potential energy.

$\vec{F_M} = -\nabla (U) = -\nabla(-\vec{\mu}\cdot\vec{B})=\nabla(\vec{\mu}\cdot\vec{B})$

Now we fill in our previous found expression for the magnetic moment.

$\vec{F_M} =\nabla(-\frac{Ze^2\vec{B}}{6m_e}\langle r^2\rangle\cdot\vec{B}) =-\frac{Ze^2}{6m_e}\langle r^2\rangle\nabla(B^2)=-\frac{Ze^2}{6m_e}\langle r^2\rangle\frac{\partial}{\partial z}(B^2)$

Notice how the force doesn’t depend anymore on the direction of the magnetic field. It only depends on the change in the square of the magnetic field, which is independent of the direction of the magnetic field. So to levitate Magneto needs to make a magnetic field that varies greatly with the height. An important thing to note, we have only information of the derivative of the square of the magnetic field this will not give us direct information of the strength of the magnetic field. In short Magneto can levitate with a magnetic field of 1T or 1mT. It is not the magnitude that matters but the shape. It is the change in magnitude in function of the height that matters. Now to get some numbers for this derivative, we need to know what the scarying factor in front is. e and m_e are fundamental constants that we can look up, 1.60e-19C and 9.11e-31kg respectively. Now we will calculate the number of electrons in magneto’s body. This is very difficult to calculate accurately but a rough estimate will suffice. The atomic composition of a human body is roughly: 65% Oxygen, 18% Carbon, 10% Hydrogen, 3% Nitrogen and 4% other. Magneto weighs around 86.18kg so from this we can calculate his atomic composition: 56.02kg Oxygen, 15.51kg Carbon, 8.62kg Hydrogen, 2.59kg Nitrogen and 3.45kg other. Then we can convert the masses to moles: 3501.1 mol Oxygen, 1291.62 mol Carbon, 8552.4 mol Hydrogen, 184.91 mol Nitrogen and 98.65 mol other. From this we can estimate the total number of electrons by multiplying the number of moles with the number of electrons the atom has in its ground state:

$Z \approx 2.8\cdot 10^{28}$

The last constant, <r^2>, is the expected value of the square distance from the electron to the nucleus. This is very difficult to calculate for every atom in Magneto’s body, so we will assume that this is given by the expected value for the squared distance of hydrogen. This assumption is only justified, because it’s simple. A better value is difficult to obtain and let’s keep things nice and simple. So for this constant we get:

$\langle r^2\rangle=8.4\cdot 10^{-21}m^2$

Plugging everything in gives us:

$\frac{Ze^2}{6m_e}\langle r^2\rangle=1.12C^2m^2kg^{-1}$

For Magneto to be stable, the total force acting on him must be zero. So the gravitational force must cancel with the magnetic force. Recall that gravitational force near the Earth’s surface is given by mass times the gravitational constant. The gravitational pull acting on Magneto is given by:

$\vec{F_g}=-m_Mg\approx -845.43N$

The minus sign indicates that the force is directed downward. So for a stable levitation point we have that the two forces cancel each other:

$\vec{F_M} = -\vec{F_g}$

Plugging everything we found so far in, gives us:

$-\frac{Ze^2}{6m_e}\langle r^2\rangle\frac{\partial}{\partial z}(B^2) = m_Mg$

$\frac{\partial}{\partial z}(B^2) = -\frac{6m_e}{Ze^2\langle r^2\rangle}m_Mg\approx -753.05\frac{T^2}{m}$

For Magneto to levitate he needs to produce a magnetic field that falls of with a ridicolous amount on the point where he wants to levitate. The Tesla is a very big unit so for the square of the magnetic field to fall with around 700 T over 1 m is a huge difference, but not impossible for the master of magnetism. Magneto has two options he can make a magnetic field with a huge magnitude difference over a reasonable distance or he can make a magnetic field with a low magnitude difference but over a really small distance. Because we have only information over the gradient, we can’t say much over the actual magnetic field. For Magneto to levitate in our 3D-world it’s more difficult, because it’s not guaranteed that the point, where gravity and the diamagnetic force cancel, is stable. Also we made some easy assumptions so the values are not really accurate, but we got a rough estimate.

I hope you enjoyed this post and till next time!

Dit delen:

Related

Leave a comment Cancel reply